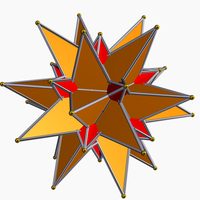
Compound of great icosahedron and great stellated dodecahedron
| Compound of great icosahedron and stellated dodecahedron | |
|---|---|
| |
| Type | stellation and compound |
| Coxeter diagram | |
| Convex hull | Dodecahedron |
| Polyhedra | 1 great icosahedron 1 great stellated dodecahedron |
| Faces | 20 triangles 12 pentagrams |
| Edges | 60 |
| Vertices | 32 |
| Symmetry group | icosahedral (Ih) |
There are two different compounds of great icosahedron and great stellated dodecahedron: one is a dual compound and a stellation of the great icosidodecahedron, the other is a stellation of the icosidodecahedron.
Dual compound
[edit]It can be seen as a polyhedron compound of a great icosahedron and great stellated dodecahedron. It is one of five compounds constructed from a Platonic solid or Kepler-Poinsot solid, and its dual. It is a stellation of the great icosidodecahedron.
It has icosahedral symmetry (Ih) and it has the same vertex arrangement as a great rhombic triacontahedron.
This can be seen as one of the two three-dimensional equivalents of the compound of two pentagrams ({10/4} "decagram"); this series continues into the fourth dimension as compounds of star 4-polytopes.
Stellation of the icosidodecahedron
[edit]This polyhedron is a stellation of the icosidodecahedron, and given as Wenninger model index 61. It has the same vertex arrangement as a rhombic triacontahedron, its convex hull.
The stellation facets for construction are:
 Facets from triangle |
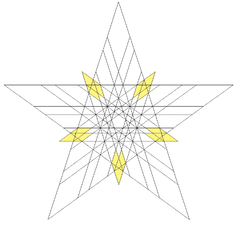 Facets from pentagon |
See also
[edit]- Compound of two tetrahedra
- Compound of cube and octahedron
- Compound of dodecahedron and icosahedron
- Compound of small stellated dodecahedron and great dodecahedron
References
[edit]- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9., p. 90.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 0-521-54325-8., pp. 51-53.
- Martyn Cundy and A. Rollett. "Great Icosahedron Plus Great Stellated Dodecahedron". §3.10.4 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 132-133, 1989.






